Definição e Propriedades dos Logaritmos matemática 1

Hoje terça feira  as aula foram de História,química,sociologia,religião,ed.física e matemática 1.

Na aula de História foi prova

Na aula de química foi laboratório 

Na aula de Sociologia foi Aristóteles

Na aula de matemática 1 foi logaritmo

Definição e Propriedades dos Logaritmos

1. Definição

A ideia que concebeu o logarítmo é muito simples, ou seja, podemos associar o termo Logaritmo, como sendo uma denominação para expoente. Dessa forma definimos de formalmente  logaritmos, da seguinte maneira:

Destacamos os seguintes elementos:

• a = Base do logaritmo;
• b = logaritmando ou antilogaritmo
• x = logaritmo

2. Consequências diretas da definição

A partir da definição de logaritmo podemos, compreender alguns resultados, que comumente denominamo de consequências da definição.

Sendo b > 0 ,a > 0 e a ≠ 1 e m um número real qualquer, temos a seguir algumas consequências da definição de logaritmo:

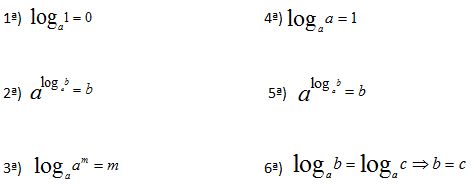
3. Propriedades dos Logaritmos

3.1 Logaritmo do produto.

Se 0 < a ≠ 1, b > 0 e c > 0, então log_a^(b.c) = log_a b + log_a c.

3.2- Logaritmo do quociente.

Se 0 < a ≠ 1, b > 0 e c > 0, então log_a^b/c  = log_a b – log_a c.

3.3- Logaritmo da potência.

Se 0 < a ≠ 1, b > 0, então  log_a(bⁿ) = n . log_ab
Exemplo de aplicação: 
Se Log 9 = x, então Log 6 é:
Solução:
Sabendo que 9 = 3², então podemos reescrever Log 9 = Log 3² = 2.Log 3 = x, portanto,
Log 3 = x/2.
Por outra lado percebe que 6 = 2.3, então, temos:
Log 6 = Log (2.3) pela propriedade 3.1, podemos escrever:
Log (2.3) = Log 2 + Log 3
Log(2.3) = Log 2 + x/2.
Resposta: Log 6 = Log 2 + x/2

Conclusão  Logaritmo é um estudo da matemática que depende  do conhecimento sobre potenciação e suas propriedades pois para encontrar o valor numérico de um logaritmo é preciso desenvolver uma potência transformá-la em um logaritmo. 

ex a x = b ↔ x = log a b 

 
Fonte https://www.infoescola.com/matematica/definicao-e-propriedades-dos-logaritmos/